In 1922, New York publisher George Arthur Plimpton made an interesting purchase from an archaeological dealer named Edgar J. Banks – a clay tablet inscribed with an example of ancient Babylonian mathematics.
Plimpton donated this piece, called Plimpton 322, and the remainder of the G.A. Plimpton Collection to Columbia University in the 1930s. Scholars have debated the mathematics behind Plimpton 322 ever since, and have only theories as to its use.

Edgar J. Banks revealed that the tablet had come from a site in southern Iraq called Senkereh, once the ancient city of Larsa. Experts believe that the tablet was written around 1800 BCE, based on the handwriting style used for its cuneiform script. More specific dating of 1822-1784 BCE has also been proposed, based on similarities with other tablets from Larsa that have dates written on them. Plimpton 322 is partly broken and is 9 centimeters tall, 13 centimeters wide, and 2 centimeters thick.

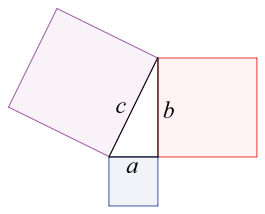
Theories propose that the author of Plimpton 322 may have been a scribe, professional mathematician, or teacher. The tablet gives an example of Pythagorean triples, in which integers a, b, and c satisfy the equation a2 + b2 = c2. The ability to make these triples can be seen as an important early achievement in mathematics because it was accomplished long before Greek and Indian mathematicians found solutions to such problems.
On the tablet is a table of numbers organized into four columns, with 15 rows of numbers in cuneiform script and Babylonian sexagesimal notation (relating to the number 60). The fourth column simply contains row numbers from 1 to 15. The second and third columns are fully visible, but the edge of the first column is broken off. In each row, the numbers in the second column are the shortest sides of right triangles, and the numbers in the third column are the hypotenuses of the triangles. The numbers in the first column give the longer sides of the right triangles. To the left of the broken-off column, there may have once been other columns.
A number of scholars have debated the interpretation and use of Plimpton 322, including Otto E. Neugebauer (1957), Buck (1980), Conway & Guy (1996), and Eleanor Robson (2002). Neugebauer believed the tablet required a number-theoretic interpretation since it gives a list of Pythagorean triples, and Conway & Guy followed this explanation. Buck gave a trigonometric explanation, but Robson argued that this explanation is based on ideas not shown in examples of the Babylonian mathematics of the time.
Eleanor Robson was given the Lester R. Ford Award by the Mathematical Association of America (MAA) for her work on Plimpton 322. Her studies differed from previous explanations of the tablet and led her to the conclusion that historical, linguistic, and cultural evidence points to an algebraic interpretation with a geometrical approach, with the table being “a list of regular reciprocal pairs”.
Robson compared another tablet from a similar time and place in her study of Plimpton 322. YBC 6967 uses quadratic equations and Plimpton 322 uses the same, reflecting mathematical methods of scribal schools of the time in a format used by period administrators. Robson demonstrated that the Plimpton 322 table is a series of worked-out exercises also seen in other examples of the era such as BM 80209. As the table’s set-up is seen on other tablets, Robson believed that the repetitive mathematical set-up would allow a teacher to create problems in the same format but with different data. Thus, she theorized that Plimpton 322’s ultimate purpose was for teachers to use the tablet as a problem set to assign to students.

In a way then, Plimpton 322 would have served as a piece of an early textbook, if one agrees with Robson’s conclusion. An ancient teacher would work off of stone tablets with patterns and problems instead of the hardcover books, paper worksheets, or iPad technology that teachers use today.
Therefore, not only is Plimpton 322 an intriguing example of the Babylonian mathematical thought and use, but it is also enlightening evidence of a culture that was developing standard educational methods and disseminating them to its teachers.
